I found a video about this experiment on Youtube, made by Veritasium and recreated it using Python in Blender.
100 prisoners are sent into a room, one by one. In this room there are as many boxes as there are prisoners and each prisoner can open half the boxes in the room. Each box contains a random number and if the prisoner finds his number in any of the 50 boxes he is allowed to open, he succeeds. Each prisoner must leave the room exactly as he found it and cannot communicate with any of the other prisoners after he's done. If any of the 100 prisoners fails, they all get executed.
The question: Is there a strategy the prisoners can agree on before the first prisoner enters the room to increase their chances of winning?
The proposed solution: Each prisoner opens the box with his number as the label first and then moves to the box with the number he finds inside that box.
For example, prisoner no. 10 enters the room, he opens box no. 10, if he indeed finds number 10 inside that box, he is done, if not he should open the box with the number he found inside box no 10 and so on.
I thought: maybe that's just one a theoretical probability experiment that only works in theory, so I whipped up this python script to test the hypothesis. I did not double-check how low the win rate is, when all prisoners pick boxes at random, because the math is pretty straight forward, so I'll assume Veritasium is right and the result it's very very low.
import numpy as np
import random
import time
print(100*"=")
prisoners = 100 # set number of prisoners here
def run(l):
for i in range(prisoners):
success = send_prisoner(l, i) #
if not success:
#print("All dead, accomplished:", i)
return False, i # i prisoners found their box before 1 failed
return True, prisoners
def send_prisoner(l, prisoner):
# let 1 prisoner search the boxes
next_box = prisoner # start with the box with index prisoner
for i in range(prisoners // 2): # each prisoner can check half the amount of boxes as there are prisoners
#print("Checking", next_box, "found:", l[next_box]) #uncomment to check if they march in loops
if l[next_box] == prisoner:
#print("Found it, tries", i) # uncomment to see how many tries it took each prisoner
return True
next_box = l[next_box]
return False
def get_boxes():
boxes = []
for i in range(prisoners):
boxes.append(i)
random.shuffle(boxes)
return boxes
# returns as many boxes as there are prisoners
boxes = np.arange(prisoners) # get a list of the numbers [0 ; prisoners -1]
np.random.shuffle(boxes) #shuffle the numbers inside the boxes
return boxes
def main():
successes = 0
total_successes = 0
start_time = time.time()
n = 1000 # how many times the warden gets his sadism on
for i in range(n):
l = get_boxes()
success, total = run(l) # run 1 experiment
#print("Run no:", i, "successes:", total)
total_successes += total
if success:
successes += 1
end_time = time.time()
win_ratio = successes / n
total_completed = total_successes / (prisoners * n)
print("Total prisoners that succeeded", total_successes, "out of: ", (prisoners * n), "=>", total_completed)
print("Win ratio:", str(round(win_ratio * 100, 3)) + '%')
print("Method took:", end_time - start_time) # so you can plan ahead how much time it would take to increase either n or prisoners
if __name__ == "__main__":
main()Running the plotted script below with n = 100,000 resulted in:
Prisoners: 2, Win rate 0.49721
Prisoners: 20, Win rate 0.32954
Prisoners: 50, Win rate 0.31907
Prisoners: 100, Win rate 0.31063
Prisoners: 200, Win rate 0.30901
Prisoners: 500, Win rate 0.30874
Prisoners: 1000, Win rate 0.30913
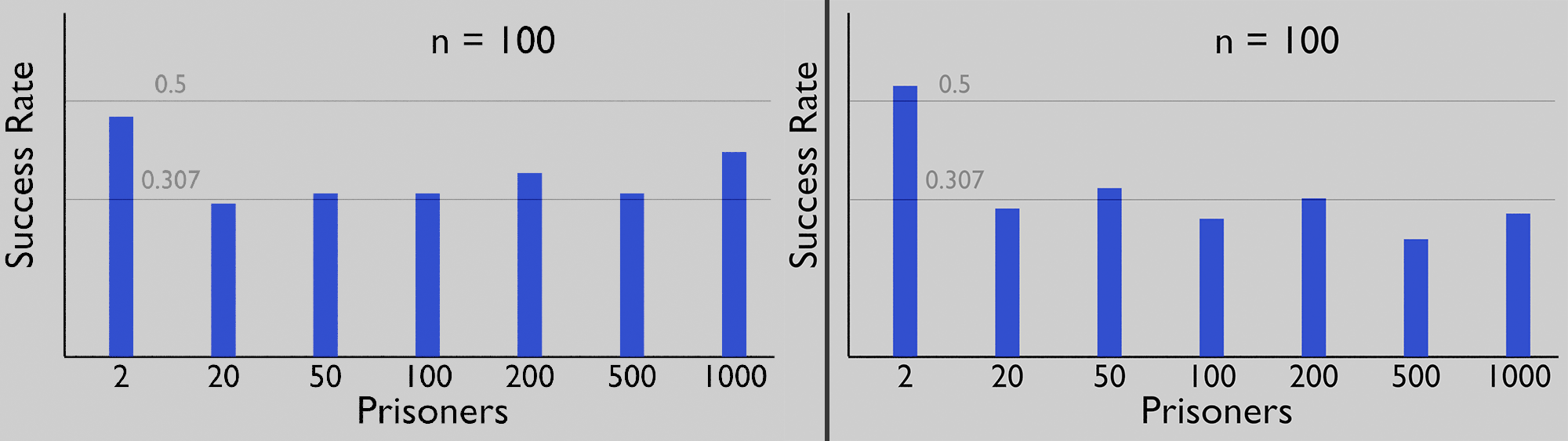
As you would expect, running the experiment 100 times is not sufficient to be statistically reliable. That would be like throwing a dye 6 times and expecting each number exactly once. This means we get a lot of fluctuation.
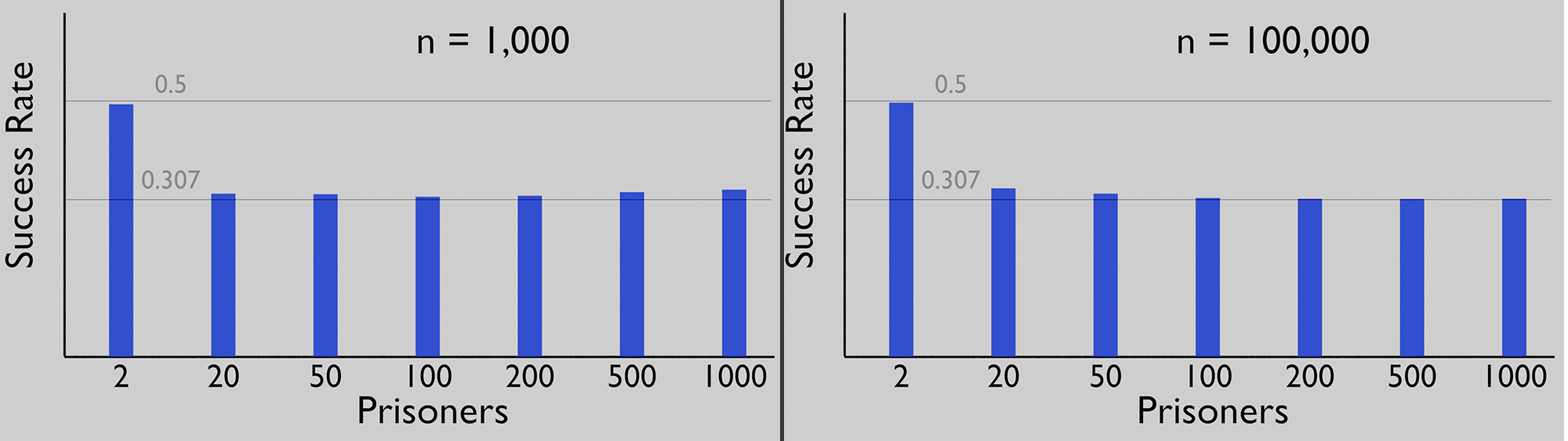
Using 1,000 iterations brings us closer to the truth and 100,000 should be sufficient to show that just like Eric claimed 100 prisoners have a success rate of ~31.1% and 1,000 still survive ~30.6% of the time.
And this wouldn't be BlenderDiplom if we would not provide the method we used to plot this in Blender, here is the script:
import random
import time
from bpy import data as D
from bpy import context as C
from mathutils import Vector
print(100*"=")
def run(l, prisoners):
for i in range(prisoners):
success = send_prisoner(l, i) #
if not success:
#print("All dead, accomplished:", i)
return False, i # i prisoners found their box before 1 failed
return True, prisoners
def send_prisoner(l, prisoner):
# let 1 prisoner search the boxes
next_box = prisoner # start with the box with index prisoner
length = len(l) // 2
for i in range(length): # each prisoner can check half the amount of boxes as there are prisoners
#print("Checking", next_box, "found:", l[next_box]) #uncomment to check if they march in loops
if l[next_box] == prisoner: # number inside the box equals the number of the current prisoner
#print("Found it, tries", i) # uncomment to see how many tries it took each prisoner
return True
next_box = l[next_box]
return False
def get_boxes(prisoners):
# returns as many boxes as there are prisoners
boxes = []
for i in range(prisoners):
boxes.append(i)
random.shuffle(boxes)
return boxes
def run_experiment(prisoners, n):
team_successes = 0 # number of times all prisoners succeded
start_time = time.time()
results = []
for i in range(n):
l = get_boxes(prisoners)
success, total = run(l, prisoners) # run 1 experiment
#print("Run no:", i, "successes:", total)
if success:
team_successes += 1
win_ratio = team_successes / n
return win_ratio
def plot(results, distance):
mesh = D.meshes['Plane'] # the base mesh for the bar, add a plane and scale it in Edit Mode
collection = D.collections['Plot']
txt_mat = None
bar_mat = None
if not 'Label' in D.materials:
txt_mat = D.materials.new('Label')
else:
txt_mat = D.materials['Label']
for i, result in enumerate(results):
prisoners = result['prisoners']
print("Prisoners", prisoners, "Win rate", result['win_ratio'])
label = str(prisoners)
txt = D.curves.new(type="FONT", name = 'Label-' + label) # need to use a font curve as object data
txt.body = label
txt.align_x = 'CENTER'
txt_ob = D.objects.new('Label-' + label, txt) # curve here, text does not work directly
txt_ob.data.materials.append(txt_mat) # so you can change the appearance of all labels at once
x = i * distance # evenly space the results
txt_ob.location = Vector((x, -1.2, 0)) #hardcoded values that fit the current setup
txt_scale = 1.3
txt_ob.scale = Vector((txt_scale, txt_scale, txt_scale))
bar = D.objects.new('Bar-' + label, mesh)
bar.scale = Vector((1, result['win_ratio'] * 20, 1))
bar.location = Vector((x, 0, 0))
collection.objects.link(txt_ob) # link the objects to the collection
collection.objects.link(bar)
def main():
start_time = time.time()
results = []
current_prisoners = [2, 20, 50, 100, 200, 500, 1000]
n = 100 # how many times the warden gets his sadism on
for prisoners in current_prisoners:
win_ratio = run_experiment(prisoners, n)
result = { # use a struct to link the current no of prisoners to their win ratio
'prisoners' : prisoners,
'win_ratio' : win_ratio
}
results.append(result)
print(prisoners, "prisoners:", win_ratio)
end_time = time.time()
print("Calculations took:", end_time - start_time) # in sec so you can plan ahead how much time it would take to increase either n or prisoners
distance = 4 # spacing between 2 bars
plot(results, distance)
if __name__ == "__main__":
main()You can probably use parts of it as snippets and even if not, it might still help you to evade the pit-fall that bpy.data.texts.new() does not create object data, you need to create a curve object data with type='FONT'.